Half Of 2 And 3/4 Cups
mymoviehits
Nov 16, 2025 · 12 min read
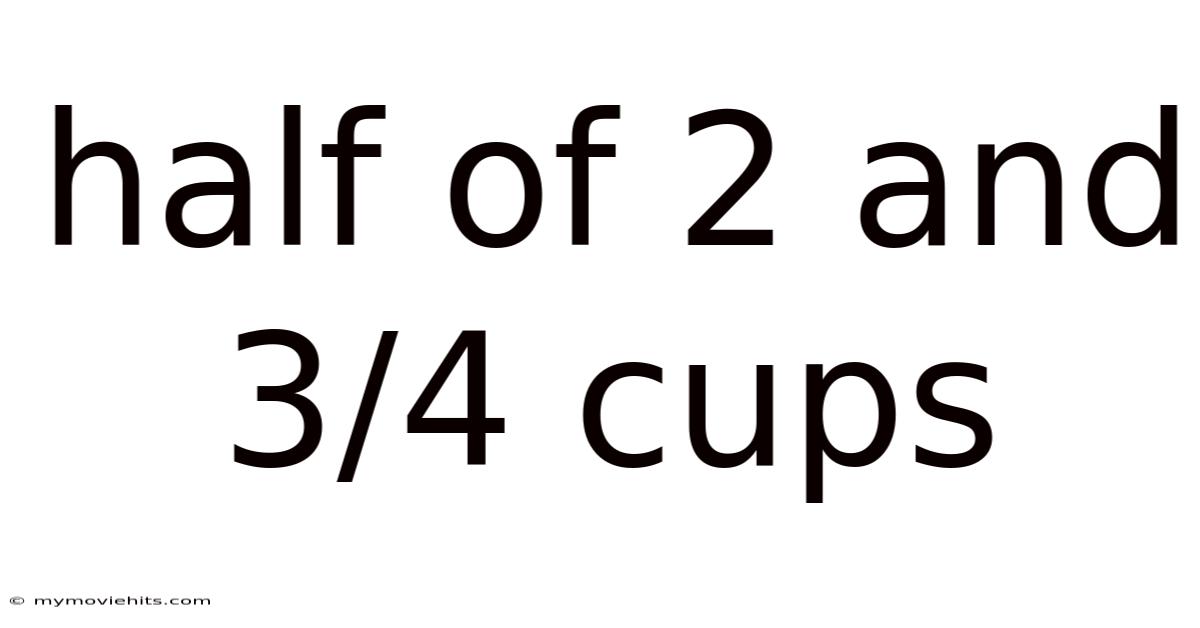
Table of Contents
Imagine you're in the middle of baking your grandmother's famous chocolate chip cookies. The recipe calls for 2 and 3/4 cups of flour, but you only want to make half the batch. The sweet aroma of vanilla and melting butter hangs in the air, urging you forward, but a nagging question lingers: what exactly is half of 2 and 3/4 cups? It seems simple enough, but when fractions enter the equation, even seasoned bakers can pause for a moment to calculate.
Understanding how to divide fractions, especially in the context of cooking or other real-world scenarios, is more than just a mathematical exercise; it's a practical life skill. Whether you are scaling down a recipe, splitting materials for a DIY project, or simply trying to understand proportions, knowing how to find half of 2 and 3/4 cups can save you time, reduce waste, and ensure your creations turn out just right. So, let's unravel this culinary conundrum and explore the ins and outs of dividing mixed fractions, ensuring that the next time you face a similar challenge, you'll tackle it with confidence and ease.
Main Subheading
The question of how to calculate half of 2 and 3/4 cups may seem straightforward, but it actually touches on several important mathematical concepts. Before diving into the specific calculation, it’s important to understand the broader context. This involves working with mixed numbers, fractions, and division, all of which are fundamental to many areas of mathematics and everyday life.
When confronted with a recipe or a project that requires scaling, the ability to manipulate fractions is crucial. Recipes, in particular, often use fractions to denote precise quantities of ingredients, and adjusting these quantities correctly can significantly impact the final result. Similarly, in fields like construction, engineering, and even art, accurate measurement and scaling using fractions are essential for achieving desired outcomes. Thus, mastering these skills isn't just about academic proficiency; it’s about enhancing practical competence and problem-solving abilities.
Comprehensive Overview
To properly understand how to find half of 2 and 3/4 cups, it's essential to break down the components and review the underlying mathematical principles. This includes understanding mixed numbers, improper fractions, and the process of division. Let's explore each of these concepts in detail.
Understanding Mixed Numbers
A mixed number is a combination of a whole number and a proper fraction. In our case, 2 and 3/4 is a mixed number. The "2" represents two whole units, and the "3/4" represents three-quarters of another unit. Mixed numbers are commonly used in everyday measurements because they provide a clear and intuitive way to express quantities that are more than a whole but less than the next whole number.
Converting Mixed Numbers to Improper Fractions
Before we can perform any mathematical operations such as division, it’s often easier to convert mixed numbers into improper fractions. An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). To convert a mixed number to an improper fraction, you multiply the whole number by the denominator and add the numerator. This result becomes the new numerator, while the denominator stays the same.
For 2 and 3/4, we would do the following: (2 * 4) + 3 = 8 + 3 = 11 So, 2 and 3/4 is equivalent to 11/4 as an improper fraction. This conversion is crucial because it simplifies the process of division and multiplication.
The Concept of Division
Division is one of the four basic arithmetic operations, and it involves splitting a quantity into equal parts. When we talk about finding "half" of something, we are essentially dividing it by 2. In the context of fractions, dividing by 2 is the same as multiplying by 1/2. This is a fundamental principle that makes fraction division much easier to handle.
Dividing Fractions: A Step-by-Step Guide
Dividing fractions might seem daunting, but it becomes simple once you understand the basic rule: To divide by a fraction, you multiply by its reciprocal. The reciprocal of a fraction is obtained by swapping its numerator and denominator. For example, the reciprocal of 2 (or 2/1) is 1/2.
So, to find half of 11/4, we multiply 11/4 by 1/2: (11/4) * (1/2) = 11/8 This gives us the result 11/8, which is an improper fraction. To make it more understandable in a practical context, we convert it back to a mixed number.
Converting Improper Fractions Back to Mixed Numbers
To convert an improper fraction back to a mixed number, you divide the numerator by the denominator. The quotient (the whole number result) becomes the whole number part of the mixed number, and the remainder becomes the numerator of the fractional part. The denominator stays the same.
For 11/8, we divide 11 by 8: 11 ÷ 8 = 1 with a remainder of 3 So, 11/8 is equivalent to 1 and 3/8 as a mixed number. This means that half of 2 and 3/4 cups is 1 and 3/8 cups.
Understanding these foundational concepts is crucial for accurately calculating fractions in various real-world scenarios. By mastering mixed numbers, improper fractions, division, and their interconversion, you can confidently tackle any mathematical challenge that comes your way, whether in the kitchen, the workshop, or beyond.
Trends and Latest Developments
While the basic principles of fraction division remain constant, the way we approach and teach these concepts is continually evolving. In recent years, there's been a growing emphasis on visual and hands-on learning methods to make fractions more accessible and less abstract for students.
One popular trend is using fraction bars or circles, which provide a visual representation of fractions and help learners understand concepts like equivalence and division more intuitively. These tools allow students to physically manipulate fractions, making it easier to grasp the underlying principles.
Another development is the integration of technology into mathematics education. Interactive software and apps can provide dynamic and engaging ways to practice fraction operations. These tools often include simulations, games, and personalized feedback, which can enhance learning outcomes.
Furthermore, there’s an increasing focus on real-world applications of fractions in curricula. Rather than just rote memorization of rules, educators are emphasizing problem-solving skills that connect fractions to everyday scenarios. This approach helps students see the relevance of what they’re learning and motivates them to master these essential mathematical skills.
Professional insights also highlight the importance of conceptual understanding over procedural knowledge. While it’s important to know how to perform fraction operations, it’s even more critical to understand why these operations work. This deeper understanding allows for greater flexibility in problem-solving and better retention of knowledge. Educators are encouraged to use questioning techniques that prompt students to explain their reasoning and justify their answers, fostering a more profound and lasting comprehension of fractions.
Tips and Expert Advice
Calculating fractions can sometimes feel like navigating a maze, but with the right strategies, you can simplify the process and avoid common pitfalls. Here are some practical tips and expert advice to help you master fraction calculations.
1. Always Simplify Fractions First
Before performing any operations, simplify the fractions involved whenever possible. Simplifying means reducing the fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common factor (GCF). For example, if you encounter the fraction 4/8, you can simplify it to 1/2 by dividing both the numerator and denominator by 4. Simplified fractions are easier to work with and reduce the chances of making errors.
Simplifying fractions not only makes calculations easier but also provides a clearer understanding of the fraction's value. For instance, recognizing that 4/8 is the same as 1/2 can help you visualize the quantity more accurately, especially when dealing with real-world measurements.
2. Convert to Improper Fractions When Necessary
When dealing with mixed numbers, converting them to improper fractions before performing multiplication or division is often the most straightforward approach. As discussed earlier, this involves multiplying the whole number by the denominator and adding the numerator to get the new numerator, while keeping the denominator the same. This step eliminates the need to juggle whole numbers and fractions simultaneously, streamlining the calculation process.
Converting mixed numbers to improper fractions simplifies complex equations and ensures that you are working with consistent units. This method is particularly useful in recipes where precision is crucial, as it reduces the potential for errors and ensures accurate results.
3. Use Visual Aids
Visual aids can be incredibly helpful, especially when you're first learning about fractions or dealing with complex calculations. Draw diagrams, use fraction bars, or create pie charts to represent the fractions involved. Visualizing fractions can make it easier to understand their values and how they relate to each other.
For example, if you're trying to find half of 3/4, drawing a circle divided into four equal parts and shading three of them can help you see that half of the shaded area is equivalent to 3/8 of the whole circle. These visual representations can make abstract concepts more concrete and accessible.
4. Practice Regularly
Like any mathematical skill, mastering fractions requires consistent practice. Work through a variety of problems involving different types of fractions and operations. The more you practice, the more comfortable and confident you'll become.
Regular practice not only reinforces your understanding of fraction concepts but also helps you develop speed and accuracy. Start with simple problems and gradually increase the complexity as you improve. Utilize online resources, textbooks, and worksheets to find a wide range of practice problems.
5. Double-Check Your Work
Always double-check your work, especially when dealing with fractions. Errors can easily occur during calculations, so it's important to verify each step to ensure accuracy. If possible, use a calculator to check your answers, but also be sure to understand the underlying principles so you can recognize when a calculator might give an incorrect result.
Double-checking your work can prevent costly mistakes, whether you're baking a cake or completing a construction project. By taking the time to review your calculations, you can ensure that your final results are accurate and reliable.
6. Understand the "Why"
Instead of just memorizing rules and procedures, focus on understanding the underlying concepts behind fraction operations. Why does multiplying by the reciprocal work when dividing fractions? Why do we need a common denominator to add or subtract fractions? Understanding the "why" will help you remember the rules more easily and apply them in different situations.
A deeper understanding of fraction concepts allows you to adapt your knowledge to novel situations and solve problems more creatively. Instead of blindly following steps, you can reason through the problem and find the most efficient solution.
7. Relate Fractions to Real-World Scenarios
Fractions are all around us, from cooking and baking to construction and finance. Whenever possible, relate fraction problems to real-world scenarios to make them more meaningful and relevant. This can help you see the practical applications of fractions and motivate you to learn more.
For example, if you're learning about adding fractions, think about combining ingredients in a recipe. If you need to add 1/2 cup of flour and 1/4 cup of sugar, you can visualize how these fractions combine to make 3/4 cup of ingredients.
By incorporating these tips and expert advice into your learning process, you can improve your understanding of fractions and become more confident in your ability to solve fraction-related problems.
FAQ
Q: What is a mixed number? A: A mixed number is a number consisting of a whole number and a proper fraction combined, such as 2 and 3/4.
Q: How do I convert a mixed number to an improper fraction? A: Multiply the whole number by the denominator of the fraction, then add the numerator. Place the result over the original denominator. For example, 2 and 3/4 becomes (2*4 + 3)/4 = 11/4.
Q: What is an improper fraction? A: An improper fraction is a fraction where the numerator is greater than or equal to the denominator, such as 11/4.
Q: How do I divide fractions? A: To divide by a fraction, multiply by its reciprocal. The reciprocal of a fraction is obtained by swapping its numerator and denominator. For example, to divide by 2/3, multiply by 3/2.
Q: How do I find half of a fraction? A: To find half of a fraction, multiply it by 1/2. For example, half of 3/4 is (3/4) * (1/2) = 3/8.
Q: Why do I need to convert mixed numbers to improper fractions before multiplying or dividing? A: Converting mixed numbers to improper fractions simplifies the calculation process and reduces the risk of errors, as it allows you to work with consistent units and avoid juggling whole numbers and fractions simultaneously.
Conclusion
Calculating half of 2 and 3/4 cups involves understanding and applying several key mathematical concepts, including mixed numbers, improper fractions, and division. By converting the mixed number to an improper fraction (11/4), multiplying by 1/2, and simplifying the result, we find that half of 2 and 3/4 cups is 1 and 3/8 cups. This exercise highlights the practical importance of mastering fractions in everyday life, whether you're scaling down a recipe or tackling other measurement-related tasks.
Now that you've refreshed your understanding of fractions, put your knowledge to the test! Try scaling some of your favorite recipes or solving fraction problems in different contexts. Share your experiences and any other tips you've found helpful in the comments below. Let's continue the conversation and help each other become fraction masters!
Latest Posts
Latest Posts
-
How To Remove Shadows On Face In Photoshop
Nov 16, 2025
-
How To Invite People To Like Your Facebook Business Page
Nov 16, 2025
-
Thank You Letter After Birthday Party
Nov 16, 2025
-
How To Save To The Icloud
Nov 16, 2025
-
People That Are Having A Worse Day Than You
Nov 16, 2025
Related Post
Thank you for visiting our website which covers about Half Of 2 And 3/4 Cups . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.